Fuzzy Logic
What is Fuzzy Logic?
Fuzzy logic is basically a form of knowledge representation suitable for notions that cannot be defined precisely, but which depends upon their contexts. In other words, fuzzy logic regards uncertain logic that has no "definite" explanation
Take for example a linguistic model, in it there may be uncertain elements to consider such as a word falling into two states hence making the logic complex. With the use of fuzzy logic, theories may be implemented here in order to make it enable the system to make a more certain decision.
When it says many-valued logic, what it means is that there can be data relationships that can be in between 1 to 0, as to where values are represented through an uncertain manner. In a Boolean system you would normally see two restrictive outcomes as to where the outcome is either a yes (1) or a no (0). However, in a system that utilizes fuzzy logic the outcome could be something in the middle:
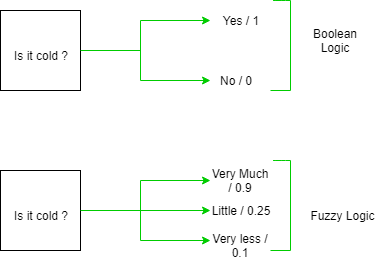
The fundamental concept of fuzzy logic is "membership functions", a membership simply defines the degree of a relationship an input value may have to an outcome/category. In the system above the membership function states that there may be input values that fall into the categories:
- Very Much
- Little
- Very Less
In terms of what membership levels are, these are basically the values in between 1~0 which enables the system to make a decision that fits into one of these membership levels. Some of these levels are more inclined onto one outcome hence making it a more certain decision. Thereafter there are other levels that point towards other directions.
Fuzzy Inference
This refers to the process of processing a fuzzy set according to a set of inference rules, and the outputting the processed set into another fuzzy set that is utilized by the systems

In the image above, there are three main processes taking place:
- Fuzzification - Takes in crisp data and converts the data into fuzzy values through the use of membership functions (a simple mathematical function used to define the degree in a which an element belongs to in a fuzzy set) and then outputs it as a fuzzy set
- Inference - Here is where the "if-then" rules occur, what the rules here do are map the degrees of truth from the fuzzy set to another set of fuzzy objects (e.g. If the temperature is hot, then the fan speed is high)
- Defuzzification - This converts the fuzzy input variables back into crisp data (e.g. High Fan Speed (Fuzzy) = 80% Speed (Crisp))
Fuzzy vs. Crisp Data
Fuzzy data is data that can be in between two solid/concrete states whereas crisp data is data that has a clear-cut membership in a set. Its memberships can represent either a single outcome such as yes or no
Fuzzy logic and crisp data are not polar opposites rather they are simply two different types of data strands that have different membership types, regard the following table:
| Data Type | Characteristics | Advantages | Disadvantages |
|---|---|---|---|
| Fuzzy | Consists of data that is between two states which handles uncertainty by simply categorizing it as a something that may be between two states | Ideal for representing real world data and more accurate in doing so, hence handling uncertain information better | More complex hence requiring more computational power to process (e.g. Processing something as simple as what a cat is could lead to considering unnecessary elements) |
| Crisp | Type of data with a certain outcome where its inputs can only be one of all its available outputs. Take for example, yes or no. This in other words may be "sharp boundaries" | Efficient for processing, storing and interpreting data for categorizatio, etc | Cannot handle or manage over complicated tasks with uncertain data hence leading to the "oversimplification" of some categories (e.g. It may assume that a tiger is cat instead of considering the smaller nuances) |
| In conclusion, fuzzy logic regards human like approximations whereas crisp data regards absolute decisions. |
Degrees of Truth
Compared to assessing the probability of something, the degree of truth simply regards how truthful an element is to its membership to a state. For example, its a hot day and given that it is a hot day it must mean that the temperature is at least 100
In other words, degrees of truth are simply the intermediate values you would have in between a true and a false value, the represent a partially true or partially false statement. Furthermore, a statement made by a person differs from the other.
One person may say "Its (0.7) hot today", while another person may mean "Its (0.9) hot today", hence defying another degree of truth that varies from person to person.
Membership Functions
A membership function maps a value to an input based on its context, e.g. If the temperature is not to warm today it might be a higher value on the "niceness" scale, hence mapping the value to something closer to a higher value in terms of the degrees of truth
Simple put, a membership function maps an input to a value to give it a more exact and fuzzified meaning. What is produced from this is known as a "fuzzy set".